Tensor stacking unplugged
Quantitative Investments
Tensor stacking is a common operation in machine learning, one that is covered by most open-source packages such as numpy, tensorflow and pytorch. However, while there is clear documentation on the syntax to stack tensors, there is no satisfactory explanation for what stacking actually does, and why results come out in a certain way.
We decided to plug the gap out there and provide a short tutorial on the subject. For us, understanding tensor stacking means being able to exactly predict, based on a set of inputs, the output that we expect to receive.
In this paper we provide a bottom-up explanation of the operation by means of a simple example. The application to more complex cases is left to the interested reader.
Tensor stacking in finance
A tensor is a higher dimensional matrix. Consider for example a spreadsheet (i.e., a 2-dimensional matrix) where constituents of a given equity market index are listed as rows, and their properties (for that day) are listed as columns, e.g., price at close, traded volume, sector, market cap, 12-months high.
Suppose you have one such spreadsheet for a number of days in the past, and that you want to feed the entire data set into a machine learning algorithm. To do so, you can decide to stack your spreadsheets ‘on top of each other’ and feed the results to your algorithm.
Alternatively, you can think of inverting the dimensions. For example, you may want to organize your data by creating one spreadsheet for each security. In said spreadsheet, rows are the days in the past and the columns are the constituent properties.
Stacking the spreadsheets thus obtained will contain the same data as before but organized in a different way. In both cases you obtain a 3-dimensional tensor (aka a cube) made of the constituent, time, and property. However, the dimensions are ordered differently. As a consequence, your machine learning outputs may differ too.
Illustrative example
Stacking is only possible among tensors of equal dimensions. Moreover, you often read that “stacking is a way to combine tensors along a new dimension”. This sentence is often mentioned to contrast stacking versus concatenating, which is another way of combining tensors that we won’t cover here.
The following example will make it clear what is meant by the sentence above. In what follows, we also provide code for you to replicate results. To do so, we chose pytorch as coding framework, but the results easily extend to other packages such as numpy and tensorflow.
Consider the following 2-dimensional tensors (each of dimensions (3,4)):
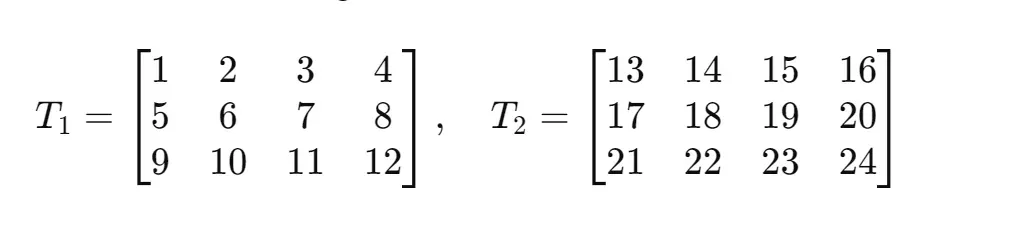
Dim 0 stacking
If we stack them on the first possible dimension (dim = 0), we obtain a 3-dimensional tensor of dimensions (2,3,4), which you can interpret as “a tensor made of two three-by-four matrices”. The parameter (dim = 0) indicates that the index running along the list of tensors to stack was put in the first possible position (i.e., position 0 in the list). That is why the first number in the resulting tensor size vector is 2, like the number of tensors we stacked.
In Python, after the usual import, the code to follow the above discussion would be:
import torch
# Create 2 tensors of dimensions (3,4) and stack them on dim = 0
T1 = torch.tensor([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
T2 = torch.tensor([[13,14,15,16],[17,18,19,20],[21,22,23,24]])
T_C0 = torch.stack((T1,T2),dim=0)
print('This is the tensor stacked on the 0 dimension:\n' + str(T_C0))
print('It has dimensions:\n' + str(T_C0.size()))
which would yield:
This is the tensor stacked on the 0 dimension:
tensor([[[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]],
[[13, 14, 15, 16],
[17, 18, 19, 20],
[21, 22, 23, 24]]])
It has dimensions:
torch.Size([2, 3, 4]).
The resulting tensor size of (2,3,4) indicates that the first index is running along the tensors in the list, and once that is chosen, the second index runs along the rows of that tensor, and the third along the columns of the same. The element (0,1,2) in the stacked denotes the (1,2) element in the first tensor1. This yields 7. Similarly, (1,2,3) are the indices corresponding to the (3,4) element in the second tensor, which is 24. To verify these claims, you can run:
# Pick an element in the combined tensor to verify
print('This is element (2,3) of tensor 1:\n' + str(T_C0[0,1,2]))
print('This is element (3,4) of tensor 2:\n' + str(T_C0[1,2,3]))
thus obtaining:
This is element (2,3) of tensor 1:
tensor(7)
This is element (3,4) of tensor 2:
tensor(24)
which is the expected result.
Dim 1 and 2 stacking
The best way to think about the output of a stacking operation with (dim = 1) is that the index running through the input tensor is now put in second position (corresponding to 1) in the output tensor. In other words, the output tensor will have size (3,2,4), which you can interpret as “a tensor made of three two-by-four matrices”.
Along the same lines, stacking with dim = 2 will result into a tensor where the index running through the input tensor is now put in third position (corresponding to 2) in the output tensor. In other words, the output tensor will have size (3,4,2), which you can interpret as “a tensor made of three four-by-two matrices”.
This code stacks the two input tensors on dim = 1 and dim = 2 respectively:
# Stacking on dims 1 and 2
T_C1 = torch.stack((T1,T2),dim=1)
T_C2 = torch.stack((T1,T2),dim=2)
print('This is the tensor stacked on the 1 dimension:\n' + str(T_C1))
print('It has dimensions:\n' + str(T_C1.size()) + '\n')
print('This is the tensor stacked on the 2 dimension:\n' + str(T_C2))
print('It has dimensions:\n' + str(T_C2.size()) + '\n')
which yields:
This is the tensor stacked on the 1 dimension:
tensor([[[ 1, 2, 3, 4],
[13, 14, 15, 16]],
[[ 5, 6, 7, 8],
[17, 18, 19, 20]],
[[ 9, 10, 11, 12],
[21, 22, 23, 24]]])
It has dimensions:
torch.Size([3, 2, 4])
This is the tensor stacked on the 2 dimension:
tensor([[[ 1, 13],
[ 2, 14],
[ 3, 15],
[ 4, 16]],
[[ 5, 17],
[ 6, 18],
[ 7, 19],
[ 8, 20]],
[[ 9, 21],
[10, 22],
[11, 23],
[12, 24]]])
It has dimensions:
torch.Size([3, 4, 2]).
The element (2,3) (in matrix terms) of the first tensor T1 is 7. To retrieve it in T_C1 we must access the index (1,0,2), which corresponds to saying “pick the element in row index 1 and column index 2 (corresponding to (2,3) in matrix terms) in the first tensor in the list (indexed at 0)”. To verify, use the following code:
# Picking element 7 (first tensor, position 2,3) in the stacked tensors
print('This is element (2,3) - in matrix terms - of tensor 1:\n' + str(T_C1[1,0,2]))
print('This is element (2,3) - in matrix terms - of tensor 2:\n' + str(T_C2[1,2,0]))
which yields, as expected:
This is element (2,3) - in matrix terms - of tensor 1:
tensor(7)
This is element (2,3) - in matrix terms - of tensor 2:
tensor(7).
Dim < 0 stacking
If you read the documentation, you will see that the parameter dim can accept negative numbers. In our example above, it can be set to have the values dim = -1,-2,-3. You may wonder, what does it do? And what is that good for?
Let’s refer to our example from above. To answer the first question, recall that the parameter dim indicates the position at which the index running through the input tensors is inserted in the final tensor dimension.
For dim = -1, it means that the index is inserted as last. In other words, negative numbers for dim indicate “counting from the back”. The output tensor will have dimensions (3,4,2), and will be identical to the output tensor above for dim = 2.
For dim = -2 and dim = -3, the output tensor will have dimensions (3,2,4) and (2,3,4) respectively. This is the same result we obtained when setting dim = 1 and dim = 0 respectively.
To convince yourself of the above, you can run:
# Stacking with negative dimensions
T_Cn1 = torch.stack((T1,T2),dim=-1)
T_Cn2 = torch.stack((T1,T2),dim=-2)
T_Cn3 = torch.stack((T1,T2),dim=-3)
print('This is the tensor stacked on the -1 dimension:\n' + str(T_Cn1))
print('It has dimensions:\n' + str(T_Cn1.size()) + '\n')
print('This is the tensor stacked on the -2 dimension:\n' + str(T_Cn2))
print('It has dimensions:\n' + str(T_Cn2.size()) + '\n')
print('This is the tensor stacked on the -3 dimension:\n' + str(T_Cn3))
print('It has dimensions:\n' + str(T_Cn3.size()) + '\n')
which yields:
This is the tensor stacked on the -1 dimension:
tensor([[[ 1, 13],
[ 2, 14],
[ 3, 15],
[ 4, 16]],
[[ 5, 17],
[ 6, 18],
[ 7, 19],
[ 8, 20]],
[[ 9, 21],
[10, 22],
[11, 23],
[12, 24]]])
It has dimensions:
torch.Size([3, 4, 2])
This is the tensor stacked on the -2 dimension:
tensor([[[ 1, 2, 3, 4],
[13, 14, 15, 16]],
[[ 5, 6, 7, 8],
[17, 18, 19, 20]],
[[ 9, 10, 11, 12],
[21, 22, 23, 24]]])
It has dimensions:
torch.Size([3, 2, 4])
This is the tensor stacked on the -3 dimension:
tensor([[[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]],
[[13, 14, 15, 16],
[17, 18, 19, 20],
[21, 22, 23, 24]]])
It has dimensions:
torch.Size([2, 3, 4])
as expected. Now, onto the second question, which we could rephrase as: “since negative values for dim give identical results to the positive values, why do we bother?”. The answer is convenience. Consider stacking two tensors of dimensions (5,4,6,8,9) each. If we wanted to stack them along the before last dimension (and thus obtain a stacked tensor or dimensions (5,4,6,8,2,9)), it might be easier to think dim = -2 as opposed to counting the exact location from the left (which would be dim = 4).
Conclusions
We hope to have clarified what stacking does. If you want to verify your understanding, try running the code above and look for the element 24. Also, in some cases, there is a geometric interpretation of the stacking operation, which you can elicit by observing how the final output is composed. Can you think of one?
1. Remember that in python the first index is 0 (and not 1). Hence, the (1,2) element in python corresponds to the (2,3) element in standard matrix notation.
Vontobel makes no representations, express or implied, regarding the accuracy or completeness of this information, and the reader accepts all risks in relying on the above information for any purpose whatsoever.