From biological to artificial intelligence

Arthur Clarke, a British science fiction writer, said that “Any sufficiently advanced technology is indistinguishable from magic”. That´s how we feel when we interacted with ChatGPT for the first time, and probably still do. But magic has its drawbacks, and it´s a thin line until you hear the same labeled as ´voodoo´. By the time that happens, human distrust becomes a hindrance on the road to global adoption. And when it comes to technology and aspects of our lives that are deeply emotional, like money for example, the risk of distrust is even higher.

The AI revolution began long ago, with the first foundational works appearing in the 1950s. Yet, it is only in recent years that some of the most influential researchers have been recognized for their contributions. On October 8th, 2024, the Nobel Prize in Physics was awarded to John J. Hopfield and Geoffrey E. Hinton for their foundational discoveries in artificial neural networks¹—technology that forms the backbone of modern machine learning and AI. This recognition marks a pivotal moment in AI’s journey from cutting-edge research to mainstream adoption.

For investors, it serves as a signal: what was once perceived as 'voodoo' has become a science backed by decades of research and now stands validated at the highest level. As developers of AI-driven investment strategies, we have a vested interest in showing investors that AI offers compelling opportunities in the field of quantitative investment strategies and is well positioned to address some of the drawbacks that have been historically attributed to the practice of quant investing.

So what´s our plan? Our aim is to provide investors with an intuition of what AI does. With comprehension comes trust, and with trust comes adoption, which means investments.

In this five-article series titled expl(AI)ning, we explore the fundamentals of AI and how it is applied in investment management. The first three articles introduce AI in general: how AI is inspired by biological intelligence, how its combination of architecture and data is surpassing traditional postulated models, and how it can excel at solving data-intensive and complex problems. In the last two articles, we shift the focus to investment management, explain how AI can enhance decision-making and show how investment decisions made by AI models can be interpreted.

Computation vs. intelligence

Back in the 1940s, computers were impressive at performing arithmetic operations and following instructions to the letter. They could calculate complex equations at unimaginable speeds for humans. However, they had a limitation: computers were rigid. They could only do what they were programmed to do and couldn’t adapt to new situations or process noisy, unpredictable data from the world around them. In short, they were good at computing, but they were not intelligent.

Researchers then set themselves on the task to build computers that could interact with their environment, handle incomplete or messy data, learn from experience, and even work in parallel—much like the human brain. To achieve this, they needed a new kind of computational model that went beyond the traditional Von Neumann architecture, a system where a computer's processing and memory are separated and work sequentially. John von Neumann outlined this architecture in his seminal 1945 paper, “First Draft of a Report on the EDVAC”², which laid the foundation for modern computing.

Today, modern personal computers are sophisticated versions of Von Neumann architectures. While this design was revolutionary at the time, it wasn't suited for tasks requiring real-time learning and adaptation, inspiring researchers to develop new models that could mimic the parallel processing capabilities of biological intelligence.

Biological intelligence

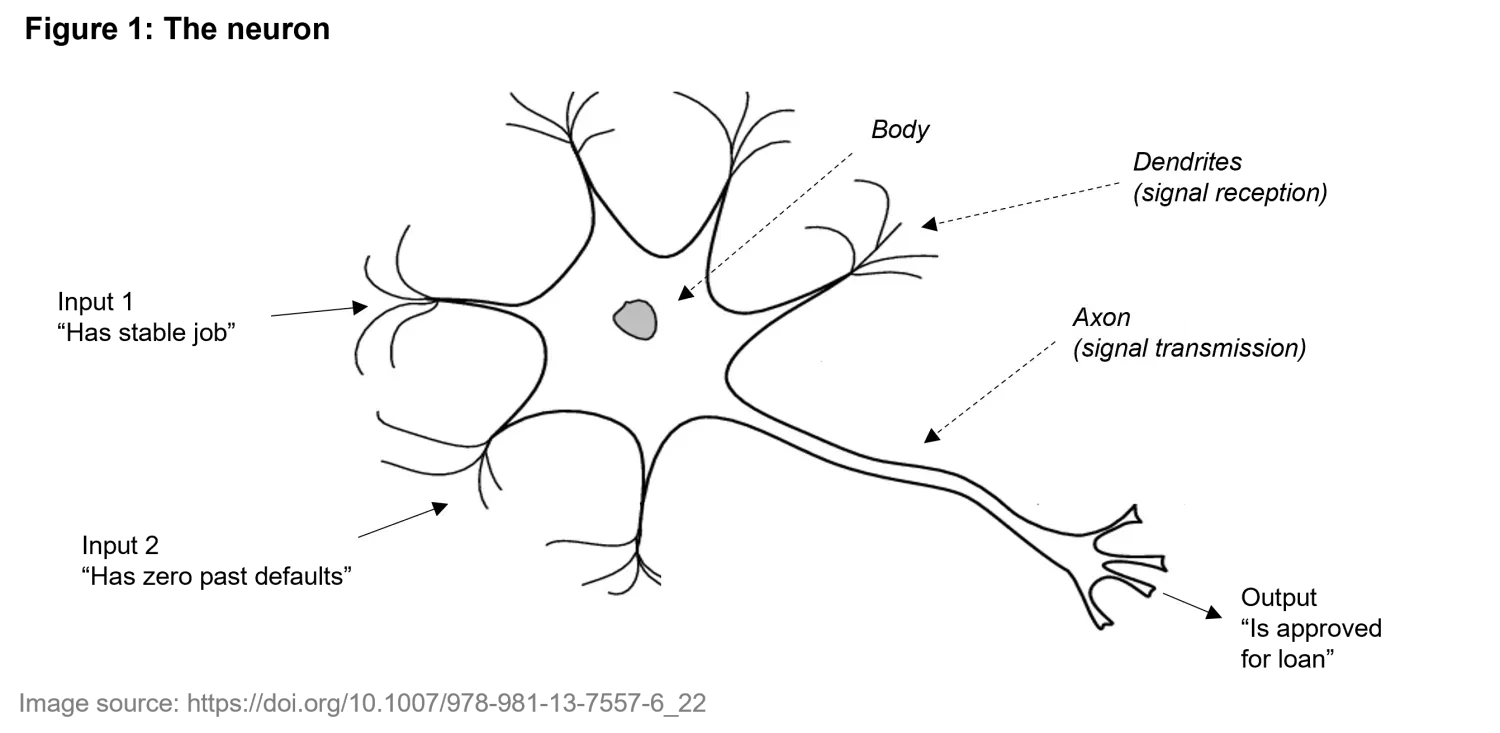
Researchers have long been inspired by biological intelligence in their quest to build more adaptive and efficient systems. At the core of this inspiration is the neuron, the fundamental building block of the brain. As shown in Figure 1 below, neurons have three core elements. They receive electrical signals through dendrites, process them in the cell body, and send outputs along the axon to other neurons.

When it comes to the processing and further transmission of incoming signals, neurons operate in a selective and non-linear manner. They only fire when incoming signals exceed a certain threshold, calibrating responses to the specific stimuli received. Taken individually, neurons are pretty rudimentary processing units. But when stacked together, like the 100 billion neurons in a human brain, magic happens. The brain is a source of wonder. It allows us to perform complex tasks, adapt, and learn. That is the kind of machine humans wanted to build. Unsurprisingly, the medical field still does not completely understand the brain.
But that´s ok. For engineers, it suffices to see that stacking individual neurons together can lead to forms of intelligence. But before we do, let’s start by understanding what we can do with a single neuron.

The single neuron

We have seen that a single neuron has a simple structure. Nevertheless, it can perform basic tasks. Consider a neuron that decides whether to approve a loan based on two characteristics: whether the applicant has a stable job and whether they have no past defaults. As shown in Figure 1, the inputs are passed to two dendrites. After receiving the inputs, the neuron combines them with specific weights (representing the importance of each characteristic) and decides to "fire" (i.e., approve the loan) if the combined inputs exceed a certain threshold. If the applicant has a stable job and no past defaults, the neuron fires from the axon (approving the loan). If either or both inputs are of low value, it remains silent (denying the loan). This process classifies the input (the applicant’s profile) as either approved or denied.

Now, let us step back and examine this operation: it represents a simple logical "and." Since it is a deterministic rule, and we only have two input variables to account for, we can enumerate all possible input combinations and plot them in a two-dimensional chart, as shown in Figure 2. We can demonstrate that the separation boundary between the approval and denial of a loan is defined by the simple linear equation on the right in Figure 2. We have formalized the separation boundary mathematically as a single neuron.

In a world where data is abundant, why limit ourselves to just two input characteristics? Let us use as many inputs as available. It is reasonable to expect that, the more we know, the better the decision will be. We also note that not all inputs may have the same importance. Knowing the applicant´s current salary may be more important than the area of their garage. But we don´t know this a priori, so we assign weights to inputs, and leave it to the machine to determine them. This thinking is what inspired Rosenblatt in 1958 when he conceived the perceptron, the first artificial intelligence model ever documented³. Figure 3 illustrates the schematics of a perceptron, along with a more generalized mathematical formulation extended to n input variables.

We´ve left one problem behind though (determining the weights), which we said we´d leave to the machine. How do we do that? Let’s go back to the loan approval example. Imagine you have historical loan data that includes various input characteristics (such as income stability, previous delinquencies, requested loan amount, currency) along with the outcome (whether the lender got their money back or not). By using specific algorithms, we can train the perceptron to recognize patterns in this data. The goal is for the perceptron to learn how different input features should be weighed to arrive at an optimal decision. Features which are more important will be given a higher weight. As the perceptron learns from past data, it can generalize this knowledge and create a model that works for new, unseen loan applications. Essentially, we feed the problem to the machine and guide it to learn which combination of inputs maximizes the likelihood of a successful loan approval.

Classification vs. regression

With the reasoning above we have introduced the perceptron for solving a very simple classification task, one of the most common tasks in AI. Classification involves categorizing data into distinct groups that are known. For instance, spam filters classify emails into "spam" or "not spam," and image recognition software can classify objects like cars or trees in photos. Classification problems involve discrete outputs, meaning the AI system assigns data to a fixed set of categories. For the perceptron, this might mean deciding between "cat" and "dog," or "yes" and "no."

On the other hand, regression problems deal with predicting continuous outcomes. Instead of assigning data to an output category, regression models predict a numerical value. For instance, a regression model might predict the price of a house based on inputs like its size, location, and number of bedrooms. Both classification and regression fall under supervised learning, where the AI system learns from labeled examples (data paired with the correct answer). There are other branches of AI as well, including unsupervised learning (where the system finds patterns without labeled data) and reinforcement learning (where the system learns through trial and error).

From perceptrons to neural networks

In Figure 3 we fed our perceptron model for loan decisions with basic data that seemed logical to us. But what if each input was in itself a more sophisticated combination of data? Our model could work better if we thought that way. For example, what if x₁ was instead the combination of employment and demographic data regarding the applicant? And since we are thinking in generic terms, why not let x₁ be the output or another perceptron that we place before the one in Figure 3? It´s easy to see that, if we iterated on this kind of thought process, we would get a stack of perceptrons connected with each other, pretty much like neurons in our brain. Welcome to the birth of multilayer perceptrons, better known as neural networks.

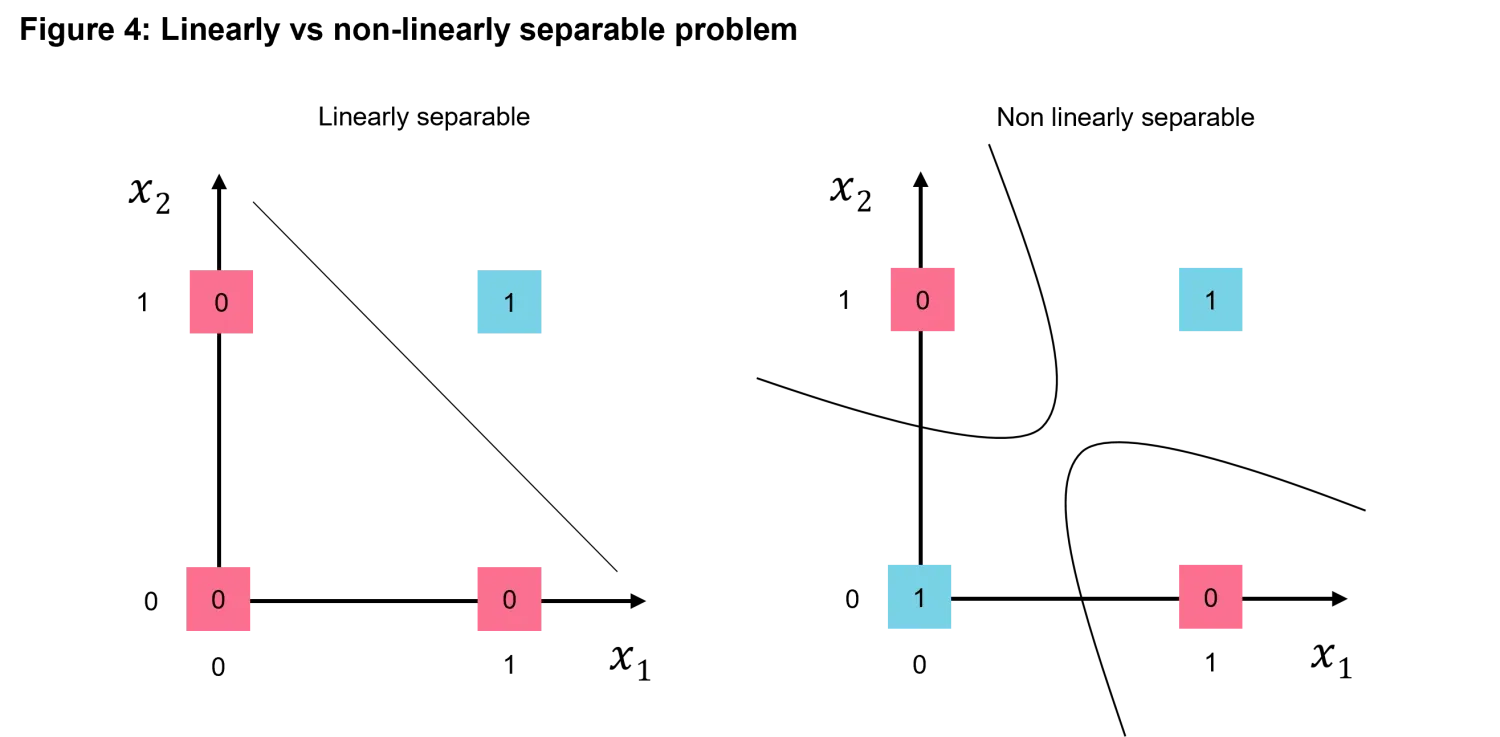
As we’ve seen in Figure 2, the perceptron works well for simple tasks like classifying data that is linearly separable, meaning it can be divided cleanly by a straight line. But what happens when the problem is more complex? How do we tackle situations where data cannot be easily separated or categorized? Or perhaps when the input variables that condition the output are in the order of tens or hundreds? For instance, in Figure 4 we compare the now known simple example of a linearly separable problem and an example of a non-linearly separable problem. Intuitively a non-linearly separable problem (in a small dimension like the one in the example) cannot be solved with a linear separation boundary.

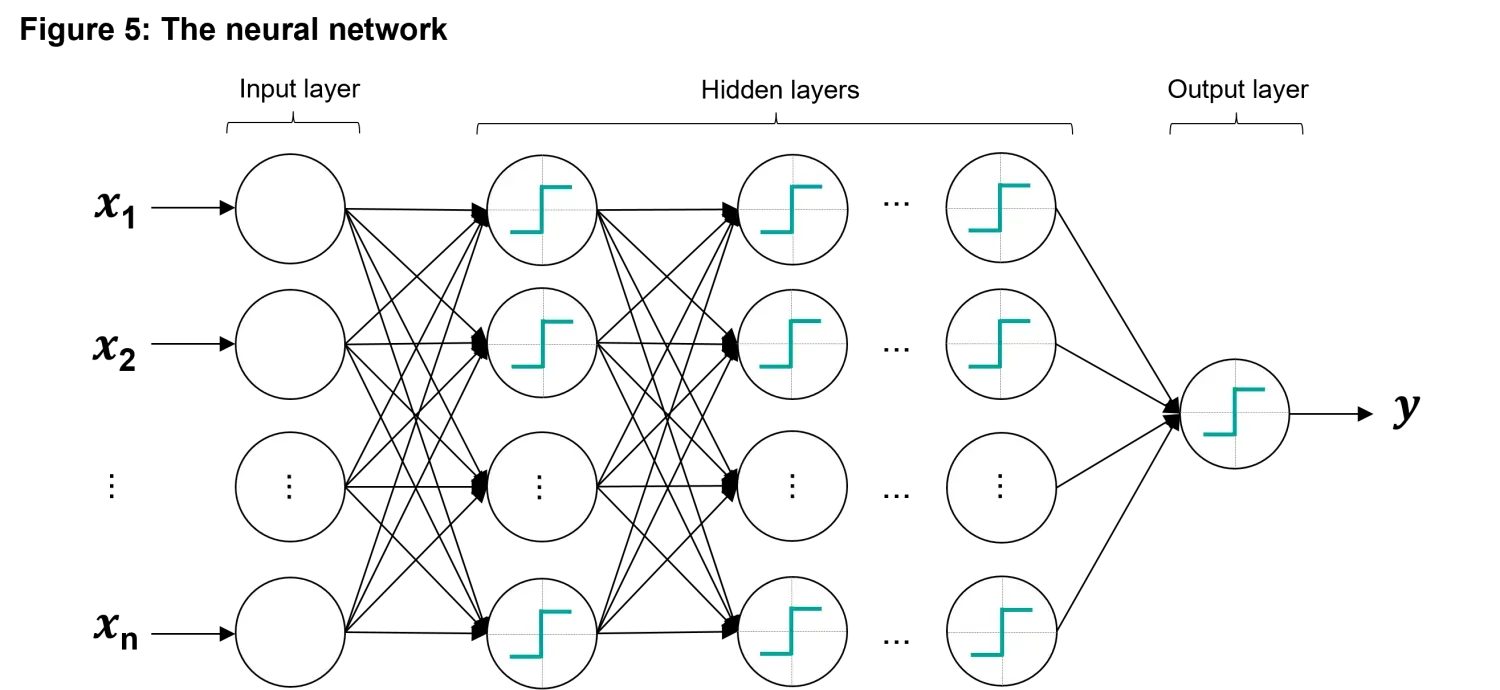
This is where neural networks come into play. By connecting multiple perceptrons together, researchers developed multilayer perceptrons – in modern terminology artificial neural networks (ANNs) – capable of handling much more complicated problems. As discussed, these networks are inspired by the brain’s ability to process information through vast numbers of interconnected neurons. Neural networks are particularly powerful because they can model non-linear relationships. They are also general-purpose, meaning they can be applied to a wide variety of tasks, from image and speech recognition to financial forecasting. In Figure 5 below we show the feed forward neural network. This network is a quite complex one that is made of an input layer of neurons that receives input variables, several hidden layers in which the non-linear interactions are captured and a final condensation output layer that goes back to the single value output.

The universal approximator

One of the most significant discoveries about neural networks is their potential as universal approximators made by Kurt Hornik in 1991⁴. The theorem states: “A single hidden layer feedforward neural network with S shaped activation functions can approximate any measurable function to any desired degree of accuracy on a compact set [of data]”. In simpler words, a neural network can learn to model any relationship between inputs and outputs, even for highly complex problems.

However, there’s a catch. While neural networks have immense potential, their performance depends on two main factors: the amount of data and the complexity of the model. If the network is too simple or the data is too limited, it might not fully learn the underlying patterns. Conversely, if the model is too complex, it might struggle to find a generalized solution, a problem known as overfitting in which the model correctly fits the input data, but its accuracy is weak when presented with new unseen input data points.

Conclusion

In this article we showed that artificial intelligence, particularly in the form of neural networks, draws significant inspiration from biological intelligence. And if we trust each other, why not trust a machine that´s built along the same architecture?

While many AI architectures exist, neural networks have garnered the most attention in recent years due to their ability to generalize and solve complex problems, such as image recognition and natural language processing. A key takeaway is that AI systems, especially neural networks, can theoretically learn to model any relationship between data points, making them highly adaptable tools for solving problems that are too complex for traditional, explicit mathematical models.

However, their success relies heavily on having enough data and selecting the right model architecture. In the next article, we will explore various AI model architectures and their distinct characteristics. We'll also challenge the notion that explicit mathematical models are always the best solution for complex problems, and instead, advocate for the importance of using the right architecture paired with the right data. Before AI became a thing, scientists won Nobel prizes by discovering equations. In the AI world, breakthroughs occur when scientists find the right architecture for the given problem. Stay tuned to find out.

1. Nobel prize in Physics press release. (www.nobelprize.org/prizes/physics/2024/press-release/)
2. Von Neumann, J. (1945). First draft of a report on the EDVAC. Moore School of Electrical Engineering, University of Pennsylvania.
3. Rosenblatt, F. (1958). The perceptron: A probabilistic model for information storage and organization in the brain. Psychological Review, 65(6), 386–408. https://doi.org/10.1037/h0042519
4. Hornik, K. (1991). Approximation capabilities of multilayer feedforward networks. Neural Networks, 4(2), 251–257. https://doi.org/10.1016/0893-6080(91)90009-T

Important Information: The content is created by a company within the Vontobel Group (“Vontobel”) and is intended for informational and educational purposes only. Views expressed herein are those of the authors and may or may not be shared across Vontobel. Content should not be deemed or relied upon for investment, accounting, legal or tax advice. It does not constitute an offer to sell or the solicitation of an offer to buy any securities or other instruments. Vontobel makes no express or implied representations about the accuracy or completeness of this information, and the reader assumes any risks associated with relying on this information for any purpose. Vontobel neither endorses nor is endorsed by any mentioned sources. AI-driven investment strategies are not available in all jurisdictions.