The Power of Many – Part I

Across domains, combining perspectives often leads to better outcomes: investors diversify portfolios, committees average expert opinions, and scientists replicate experiments across labs. The same intuition carries over to forecasting. Rather than relying on a single source of insight, pooling multiple views can help reduce errors, improve robustness, and increase confidence in results. In artificial intelligence (AI) and machine learning, this principle takes the form of model ensembles—powerful techniques that combine multiple models to improve predictive accuracy and robustness. Typical use cases include stock return forecasting (predicting future price movements for trading strategies), risk modeling (combining multiple volatility models for better risk assessment), or credit scoring & fraud detection (aggregating models to improve classification accuracy).

This article is the first part of a two-part series on model ensembles. In this opening piece, we will take a step back and explore the theoretical foundations of why combining forecasts tends to improve predictive accuracy. To do so, we draw connections between classic forecasting literature and contemporary machine learning methods, showing that many of the insights that once applied to human-based survey forecasts (e.g., on GDP or inflation) remain relevant when working with machine-based models.

In the second part of the series, we will move from theory to practice, discussing how to construct ensemble models in machine learning and exploring successful applications in financial forecasting.

Understanding Why Model Ensembles Can Improve Predictions

The idea of combining different forecasts is an old one that appeared in the literature long before machine learning techniques became popular. In 1906 Francis Galton made a famous discovery about the “wisdom of the crowds” (Figure 1). At a livestock fair, Galton collected nearly 800 guesses from visitors who tried to estimate the weight of an ox. Individually, many estimates were far off the mark, but when Galton calculated the average of all guesses, the result was astonishingly accurate—closer to the true weight than any single participant. While not a statistical model in the modern sense, this example captures the same intuition behind ensemble methods: diverse and imperfect estimates, when aggregated, can outperform even the most skilled individual predictor.

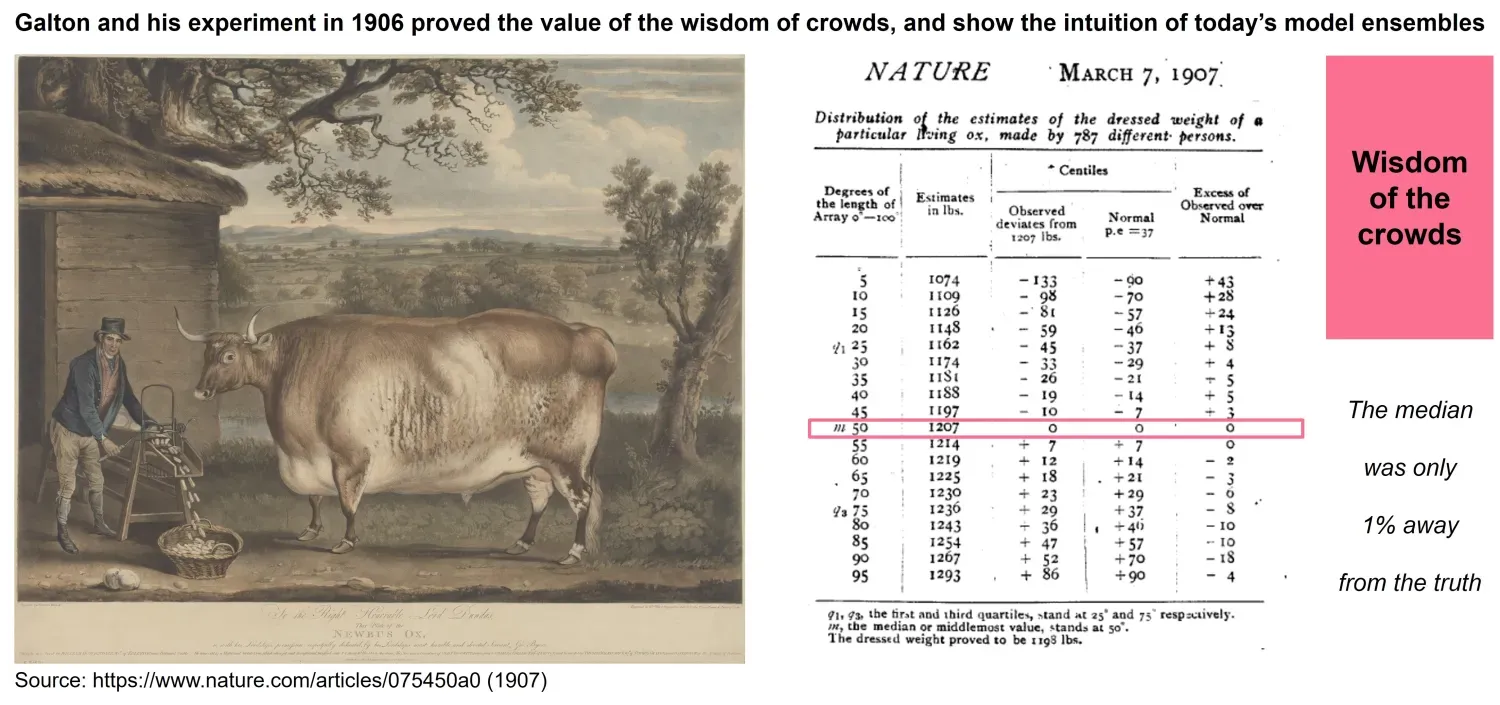
This intuition was later formalized in the forecasting literature. Timmerman (2006) provides an overview of how combining forecasts consistently improves predictive accuracy. Three main mechanisms explain this increased power:

I - Increased information efficiency: Bates and Granger (1969) already showed how combined forecasts better predict a variable of interest than the individual forecast components. An early argument in favor of forecast combinations is that the forecast user cannot observe all information that the forecasters have access to. Accordingly, only a combined forecast takes the full information set into account, which in turn improves accuracy. Intuitively, the more the information sets used overlap, the fewer improvements can be expected from combining forecasts (Clemen, 1987).

II - Robustness to shifts in the underlying process: Another channel through which forecast combinations can improve accuracy was proposed by Figlewski and Urich (1983), Kang (1986), Diebold and Pauly (1987), among others. The idea is that different forecasters use different models, which in turn are differently affected by structural breaks or regime shifts. A combination of models is naturally better able to account for such changes in the underlying process.

III - Robustness to model misspecification: More generally, all forecast models are necessarily simplifications of the real world and are thus imperfect, even in the absence of structural breaks and regime shifts. Clemen (1989) suggests that it is unlikely that one model outperforms all other models in all possible scenarios. Similar to the classic portfolio diversification argument, the errors stemming from model misspecification can be diversified to some extent by combining multiple forecasts (Makridakis and Winkler, 1983). An example of model misspecification is when a linear relationship is assumed, but the “true” relationship is actually non-linear. However, due to the low signal-to-noise ratio in financial data, it is generally difficult to precisely pin down the relationship between a predictor and the target variable. Relatedly, Makridakis (1989) points out that combinations make the forecast less dependent on the specific procedure implemented to select a model specification, thus reducing the problem of overfitting and helping to improve out-of-sample forecasts.

While the original arguments were developed with traditional econometric models in mind, the underlying mechanisms are not limited to that context. They also resonate with today’s predictive modeling practices. For a data scientist who wants to train a machine learning model based on a common data set, the increased information efficiency channel is clearly not relevant to motivating model ensembles. After all, each model can be trained on the same information set. However, the “classic” literature suggests that the two other mechanisms can make model combinations favorable. First, machine-based forecasts will also suffer from general forms of model misspecification and benefit from more “diversified” predictions. Second, machine learning algorithms will also face the challenge of structural shifts in the data they aim to forecast. Thus, we see sound theoretical reasons to expect that machine learning also benefits from model ensembles.

Closing Thoughts

In this first part of the series, we revisited the long-established idea that combining forecasts can yield more accurate predictions than relying on individual models alone. The classic mechanisms—robustness against structural shifts and protection against model misspecification—remain highly relevant for machine learning ensembles today.

But knowing why ensembles work is only the first step. In the second part of this series, we will turn to the practical side: how to actually build ensemble models, what design choices matter, and how ensembles are being applied in financial forecasting to deliver real-world results.