Will AI ever crack investing?

In our previous articles, we explored the basic principles of AI and how various neural network architectures adapt to complex datasets and problems. Today, in our third piece of the Expl(AI)ning series on AI, we address a question that’s often asked by finance professionals and AI enthusiasts alike. AI is delivering remarkable results in so many areas like vision and natural language processing, so why don’t we see AI-powered funds consistently delivering 3% excess returns per month without ever experiencing losses?

We believe that the answer lies in the concept of complexity. While AI has indeed managed to dominate fields once thought unconquerable for machines—such as interpreting image and natural language data—the complexity of financial markets introduces unique challenges that go beyond these structured environments.

To explain why that is, and more importantly, quantify where AI may be in the path of ‘solving’ the investment problem, in this article we draw a parallelism between investing and games. We’ll frame investing as a game, quantify its complexity, and see which complexity AI is currently able to solve. The conclusion? We’re not there yet. How far are we? Read further to find out.

Game complexity

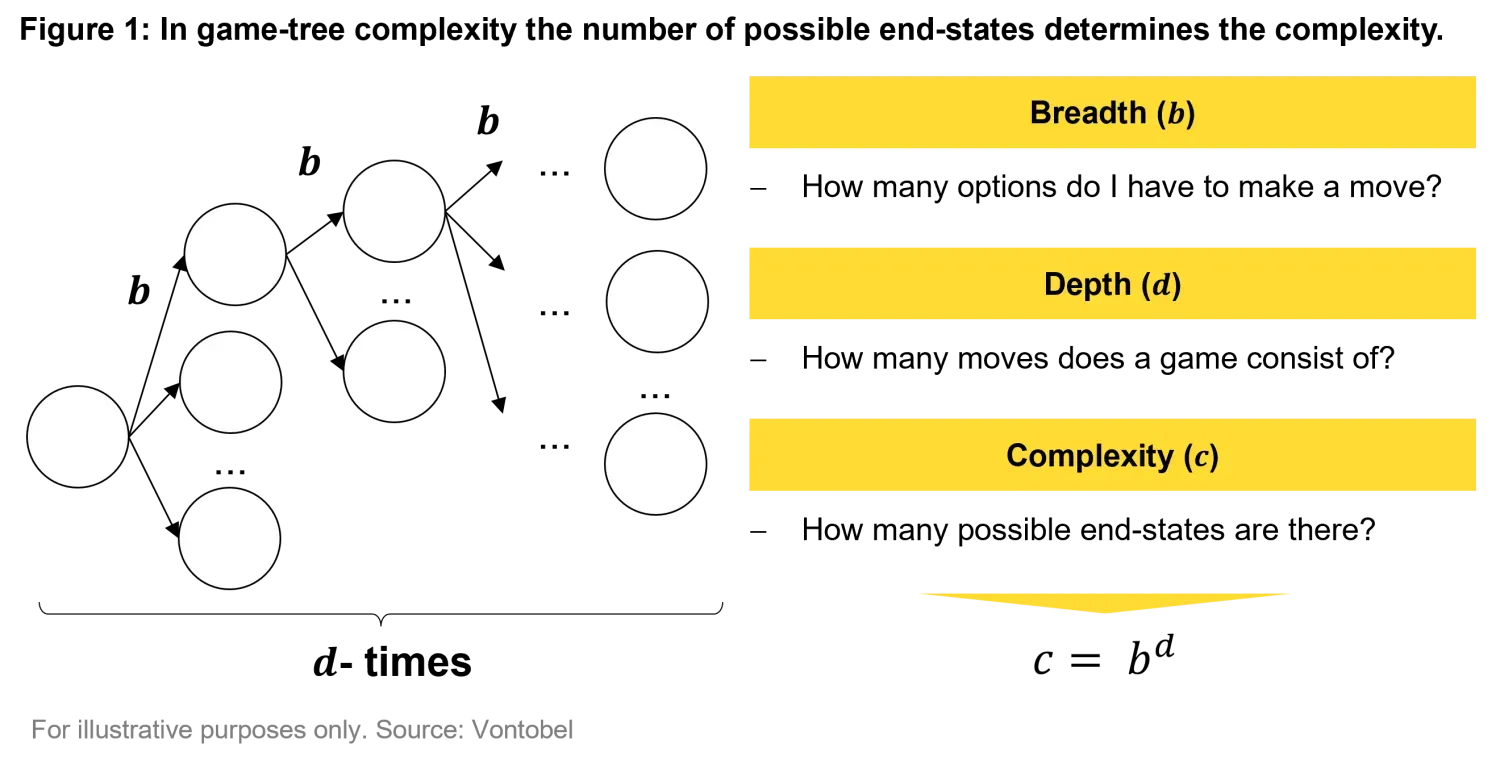
There are various ways to measure the complexity of a game. A simple intuitive one is to count the number of possible final states of the game. This methodology is called game-tree complexity¹. The more possible final states you have, the more complex the game is. So goes the intuition. Remember the exercise about determining how many pictures can you take of n students lined in a row? That is the direction. Recall that the solution to the student picture is n! (basically, given by all the possible permutations of students), that is, complexity grows quickly with the number of elements at play.

In a game, the number of final states is a function of breadth and depth. Breadth is the number of options available at each move (how many possible moves can I make when it’s my turn?), while depth is the total number of moves in a game (how long does a game last on average). As shown in Figure 1 below, the number of possible states is then given by game breadth elevated to the game depth. Let’s now use a couple of common games as examples.

Chess

Chess has long been considered a game of great complexity. However, it has a finite set of rules, a fixed board, and a well-defined objective: to checkmate the opponent's king. Also, it’s transparent: you see the opponent pieces, and they see yours.

The complexity of chess can be measured following the framework presented above by making a couple of simple assumptions. In chess the breadth changes during the game. It starts around 20 and increases as the pieces are moved around the board. Overall, 35 is considered to be a representative number of average breadth. Depth can vary a lot as well. Good chess players can close a game with an average of around 80 moves. Using the framework described above, the complexity of chess can be estimated¹ as 35⁸⁰, which is about 10¹²³.

In the late 1990s, IBM’s Deep Blue defeated Garry Kasparov, the reigning chess world champion, by leveraging brute-force computation and immense processing power. This was an historic demonstration of the potential of computers. Still, the solution was found by calculating millions of potential moves ahead rather than through any "understanding" of the game as a human would experience it. This approach was clearly not scalable and applicable to other problems or games.

Go

Go, unlike chess, features a much larger board and a much higher number of possible move sequences, making a brute-force approach unfeasible. The complexity of Go can also be measured using the very same framework, obviously by using breadth and depth parameters that are typical of the game. In Go, the breadth (number of possible moves per turn) is significantly larger than chess due to the size of the board (19x19). At the beginning of the game, there are 361 possible moves, but as stones are placed, this number decreases. On average, 250 is considered a reasonable estimate. The depth of Go refers to the number of moves in a complete game. While the theoretical maximum depth can be over 500 moves, skilled players tend to finish games in around 150 moves. Using these assumptions, the complexity of Go can be estimated¹ as 250¹⁵⁰, or 10³⁶⁰, far surpassing the complexity of chess. This explains why we had to wait almost two decades for computers to dominate the more complex board game Go.

When DeepMind’s AlphaGo defeated Go champion Lee Sedol in 2016, it was a marked as a moment in AI history. Instead of calculating every possible move – like IBM did for chess – AlphaGo used neural networks to evaluate the board and predict the best moves based on patterns it had learned from millions of games. This required a combination of deep learning and reinforcement learning techniques, allowing AlphaGo to "learn" from past games in a way that simulated experience.

Go’s success demonstrated that AI could go beyond mere computational power—it could develop adaptive strategies by “learning” from experience. This was a significant step up from chess, as Go’s near-infinite possibilities required a more abstract understanding. But even Go remains, in essence, a structured game with a clear goal and fixed parameters.

Investing

While chess and Go are incredibly complex, investing introduces unique forms of complexity. First, financial markets lack a fixed set of rules, as market forces are constantly evolving, influenced by countless unpredictable factors like geopolitical events, market sentiment, and human behaviour, all of which that can change the rules of the game “overnight”. The objective in investing isn’t as straightforward as winning a game. Instead, it’s about maximizing returns, managing risk, and adapting to changing conditions, all while contending with the unpredictability of real-world events. In short, every participant in the investing game shows up at game night with a totally different set of objectives and – literally – chips on the table.

Financial markets can be framed as a game in which "players" (investors) make investment decisions based on market information, rules (regulations), and objectives (e.g., maximizing returns, minimizing risk). Each decision involves choosing from a vast array of possible investments (securities) while navigating the passage of time (investment horizon). Using this perspective, we can estimate the complexity of financial markets by considering the breadth (number of possible investment choices) and depth (length of the investment horizon). In this article we focus on equity markets as an example.

In this framework for instance, the breadth of equity markets can be represented by the total number of publicly listed companies worldwide, estimated² at around 54’000. This includes equities from all over the globe. The depth corresponds to the length of the average investment period. Consider a CIO of an equity investments franchise, we can estimate the average career to be 10 years long or approximately 2’000 trading days (assuming 200 trading days per year). Supposing that our example CIO makes one investment decision per day, the game's complexity can be calculated by combining these factors.

With a breadth of 54’000 choices per day and a depth of 2’000 days, the complexity of financial markets can be estimated to be on the order of 10^9’500. This (conservative) estimate underscores the immense number of possible decision paths that an investor is facing. This is where leveraging advanced tools like machine learning and artificial intelligence is becoming increasingly critical for market analysis and investment decision-making to make sense of this complexity.

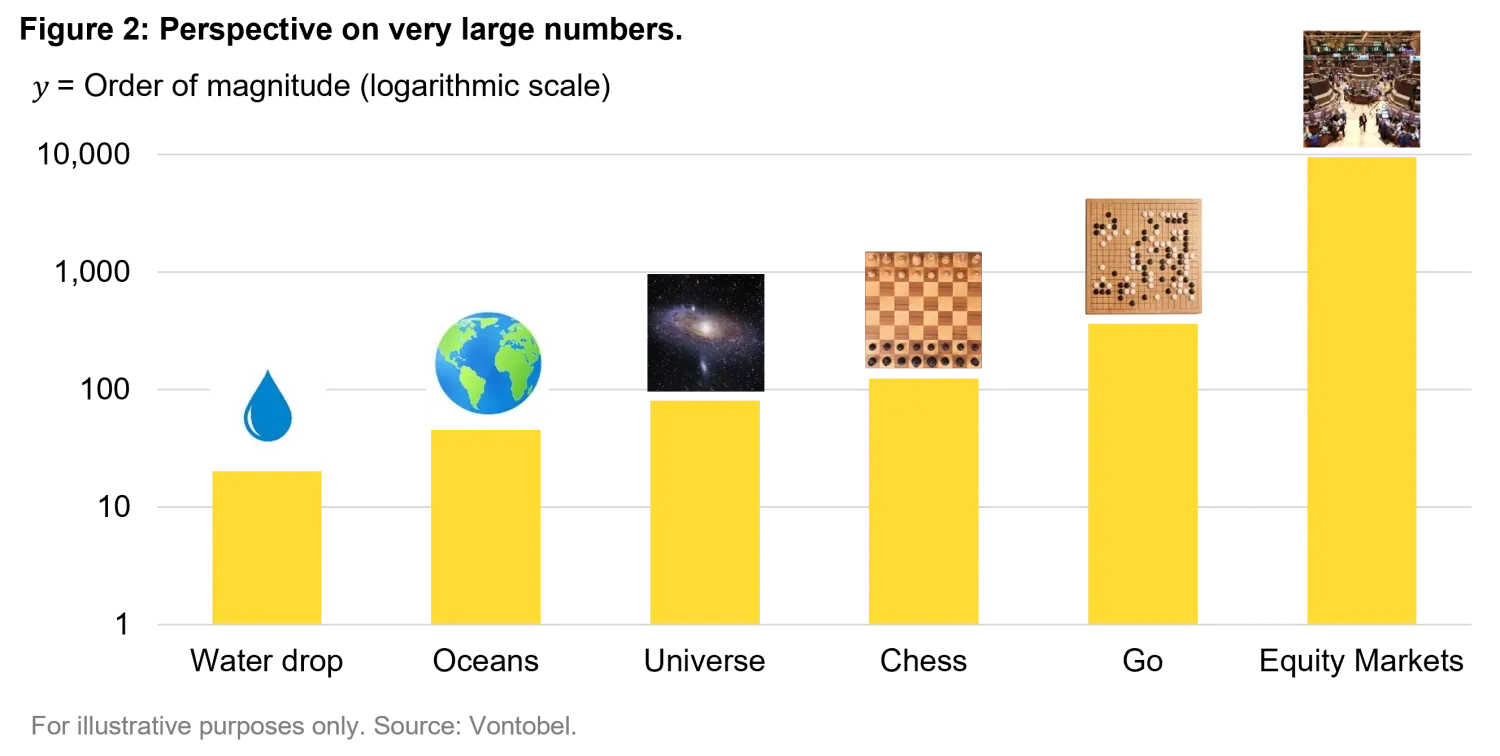
In Figure 2 we put things into perspective to give you an idea of how big the complexity we just measured is. One single drop of water contains approximately 10²¹ molecules of water³. Now, stop for a second and try to guess the total number of water molecules on earth. You might be tempted to say it’s some crazy 10^{1’000’000} number when it’s just around 10⁴⁰. The total number of atoms on planet earth⁴ is around 10⁵⁰ meanwhile the milky galaxy is estimated to contain 10⁶⁷ atoms⁵. The takeaway here is that representing very large numbers (that are hard to imagine) might trick you to think that they are very close when there is an exponential size difference. These numbers are not even close to the complexity of financial markets as we measured it 10^9’500 is still 10⁹⁴³³ times larger than the number of atoms in the galaxy!

In investing, there are no guaranteed moves or consistent outcomes. Market patterns that worked in the past may no longer apply in the future. This is the core of the investing’s complexity: while AI has succeeded in environments with fixed rules and structured goals, the financial markets present a chaotic, open-ended system with few constraints.

Why games were easier to crack

Reflecting on the successes of AI in solving Go, one might wonder why these achievements haven’t directly translated to investing. The key difference is that in games, every move and response is part of a defined environment, which can be gradually mastered through data and experience. The only variability at play lies in the choice of the next move, which is made by one individual.

Investing, on the other hand, operates in an open system where tomorrow’s “rules” can shift in ways that even the most sophisticated algorithms struggle to anticipate. This is the concept of non-stationarity, or when the “rules” (or probability distributions) that regulate a game change in time. Cracking non-stationary problems is among the most complex things to do.

Also, let’s not forget that investing, as a science – despite the vast magnitude of numbers at play (after all, it’s an industry that ingests numbers to produce numbers) – is closer to a ‘social’ science than a ‘hard’ science like physics or chemistry. The outcome, or the price of a security, is the result of multiple bids on the security, not the ‘moves’ of a single individual. And as such, there may be a limit to the amount of structure that can be discoverable. 

Yet, this doesn’t mean AI hasn’t made strides in investments. AI-driven quantitative models, high-frequency trading, and algorithmic strategies have become commonplace on trading floors worldwide. However, no AI system has yet managed to deliver consistent, high returns month after month without risk of losses (that we heard of or that is public for everyone to buy). Long story short: as we already saw in our previous piece, there is not one AI that solves it all, yet. While AI has certainly improved financial modelling and trading efficiency, the inherent unpredictability of human-driven markets makes investments still an open challenge that should be addressed with continuous improvements.

Conclusion

The overarching message here is that investing remains a realm of complexity greater than even games like chess and Go. But if AI has been able to master such intricate games, why not finance? The answer, it seems, is not a limitation of AI itself but a reminder of the unique characteristics of the markets. Investing involves managing risk, adapting to unforeseen events, and balancing various objectives, making it inherently more complex than structured games. However, if we apply AI’s capabilities thoughtfully, there is potential to harness its power in a way that supports financial decision-making.

In the next piece, we will dive into a practical use case: enhancing traditional factor investing with AI. While classic factor investing focuses on identifying and explaining persistent sources of returns based on historical data, integrating AI allows us to adapt these factors to current market conditions in real time and produce meaningful forecasts. This hybrid approach could make factor investing more flexible and responsive bridging some of the complexity gap we’ve discussed earlier in the article.

Stay tuned as we explore how AI, when applied judiciously, might indeed unlock new paths for consistent and adaptive investment strategies.